1 概念

分治算法，根据字面意思解释是“分而治之”，就是把一个复杂的问题分成两个或更多的相同或相似的子问题，再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。

2 算法策略

分治策略：对于一个规模为 n 的问题，若该问题可以容易地解决(比如说规模 n 较小)则直接解决，否则将其分解为 k 个规模较小的子问题，这些子问题互相独立且与原问题形式相同，递归地解这些子问题，然后将各子问题的解合并得到原问题的解。

在平时日常生活中，分治思想也是随处可见的。例如：当我们打牌时，在进行洗牌时，若牌的数目较多，一个人洗不过来，则会将牌进行分堆，单独洗一小堆牌是相对容易的，每一堆牌都洗完之后再放到一起，则完成洗牌过程。

3 使用场景

(1)该问题的规模缩小到一定的程度就可以容易地解决。

(2)该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质。

(3)利用该问题分解出的子问题的解可以合并为该问题的解。

(4)该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子问题。

4 基本步骤

分治法在每一层递归上都有三个步骤：

(1)分解：将原问题分解为若干个规模较小，相互独立，与原问题形式相同的子问题。

(2)求解：若子问题规模较小而容易被解决则直接解，否则递归地解各个子问题。

(3)合并：将各个子问题的解合并为原问题的解。

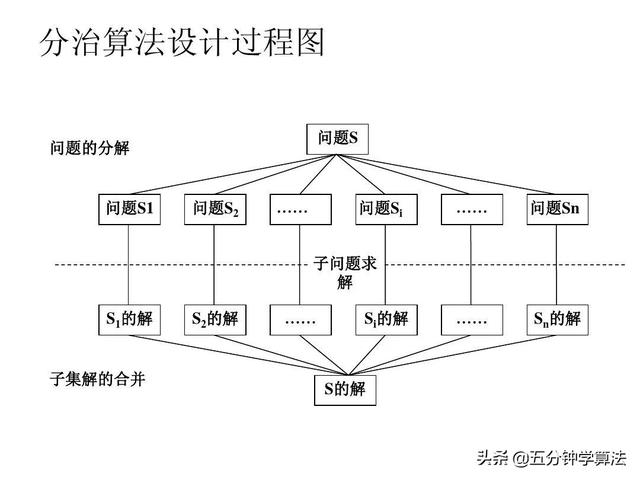
分治思想

5 伪代码

 Divide-and-Conquer(P) if |P| ≤ n0 then return(ADHOC(P)) 将P分解为较小的子问题 P1 ,P2 ,...,Pk for i←1 to k do yi ← Divide-and-Conquer(Pi) △ 递归解决Pi T ← MERGE(y1,y2,...,yk) △ 合并子问题 return(T)

其中，|P| 表示问题 P 的规模，n0 为一阈值，表示当问题 P 的规模不超过 n0 时，问题已容易直接解出，不必再继续分解。ADHOC(P) 是该分治法中的基本子算法，用于直接解小规模的问题 P。因此，当 P 的规模不超过n0 时直接用算法 ADHOC(P) 求解。算法 MERGE(y1,y2,…,yk) 是该分治法中的合并子算法，用于将 P 的子问题 P1 ,P2 ,…,Pk 的相应的解 y1 , y2 ,…, yk 合并为 P 的解。

6 典型案例

6.1 二分查找

二分查找是典型的分治算法的应用。需要注意的是，二分查找的前提是查找的数列是有序的。

算法流程：

(1)选择一个标志 i 将集合分为二个子集合。

(2)判断标志 L(i) 是否能与要查找的值 des 相等，相等则直接返回。

(3)否则判断 L(i) 与 des 的大小。

(4)基于判断的结果决定下步是向左查找还是向右查找。

(5)递归继续上面的步骤。

通过二分查找的流程可以看出，二分查找是将原有序数列划分为左右两个子序列，然后在对两个子序列中的其中一个在进行划分，直至查找成功。

代码实现：

#include#includeint k;int binarysearch(int a[],int x,int low,int high)//a表示需要二分的有序数组(升序)，x表示需要查找的数字，low，high表示高低位{ if(low>high) { return -1;//没有找到 } int mid=(low+high)/2; if(x==a[mid])//找到x { k=mid; return x; } else if(x>a[mid]) //x在后半部分 { binarysearch(a,x,mid+1,high);//在后半部分继续二分查找 } else//x在前半部分 { binarysearch(a,x,low,mid-1); }}int main(){ int a[10]={1,2,3,4,5,6,7,8,9,10}; printf("请输入需要查找的正数字："); int x; scanf("%d